Fisica 3 - Relacion de trabajo (adiabatico) con la temperatura de una masa de agua

Gráfico de un proceso adiabático en función de p y V.

En termodinámica se designa como proceso adiabático a aquel en el cual el sistema (generalmente, un fluido que realiza un trabajo) no intercambia calor con su entorno. Un proceso adiabático que es además reversible se conoce como proceso isentrópico. El extremo opuesto, en el que tiene lugar la máxima transferencia de calor, causando que la temperatura permanezca constante, se denomina como proceso isotérmico.

El término adiabático hace referencia a elementos que impiden la transferencia de calor con el entorno. Una pared aislada se aproxima bastante a un límite adiabático. Otro ejemplo es la temperatura adiabática de llama, que es la temperatura que podría alcanzar una llama si no hubiera pérdida de calor hacia el entorno. En climatización los procesos de humectación (aporte de vapor de agua) son adiabáticos, puesto que no hay transferencia de calor, a pesar que se consiga variar la temperatura del aire y su humedad relativa.

El calentamiento y enfriamiento adiabático son procesos que comúnmente ocurren debido al cambio en la presión de un gas. Esto puede ser cuantificado usando la ley de los gases ideales.

Enfriamiento adiabático del aire

Existen, tres relaciones en el enfriamiento adiabático del aire:

La relación ambiente de la atmósfera, que es la proporción a la que el aire se enfría a medida que se gana altitud.
La tasa seca adiabática, es de unos -1° por cada 100 metros de subida.
La tasa húmeda adiabática, es de unos -0,6° - 0,3º por cada 100 metros de subida.

La primera relación se usa para describir la temperatura del aire circundante a través del cual está pasando el aire ascendente. La segunda y tercera proporción son las referencias para una masa de aire que está ascendiendo en la atmósfera. La tasa seca adiabática se aplica a aire que está por debajo del punto de rocío, por ejemplo si no está saturado de vapor de agua, mientras que la tasa húmeda adiabática se aplica a aire que ha alcanzado su punto de rocío. El enfriamiento adiabático es una causa común de la formación de nubes.

El enfriamiento adiabático no tiene por qué involucrar a un fluido. Una técnica usada para alcanzar muy bajas temperaturas (milésimas o millonésimas de grado sobre el cero absoluto) es la desmagnetización adiabática, donde el cambio en un campo magnético en un material magnético es usado para conseguir un enfriamiento adiabático.

Formulación matemática

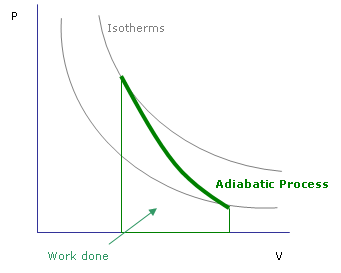
Durante un proceso adiabático, la energía interna del fluido que realiza el trabajo debe necesariamente decrecer

La ecuación matemática que describe un proceso adiabático en un gas es

$P V^{gamma} = operatorname{constante} qquad$

donde P es la presión del gas, V su volumen y

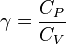
$gamma = {C_{P} over C_{V}}$

siendo $C P$ el calor específico molar a presión constante y $C V$ el calor específico molar a volumen constante. Para un gas monoatómico ideal, $γ = 5 / 3$ . Para un gas diatómico (como el nitrógeno o el oxígeno, los principales componentes del aire) $γ = 1,4$

Derivación de la fórmula

La definición de un proceso adiabático es que la transferencia de calor del sistema es cero, $Q = 0$ .

Por lo que de acuerdo con el primer principio de la termodinámica,

$Delta U + W = 0 qquad qquad qquad (1)$

donde U es la energía interna del sistema y W es el trabajo realizado por el sistema. Cualquier trabajo (W) realizado debe ser realizado a expensas de la energía U, mientras que no haya sido suministrado calor Q desde el exterior. El trabajo W realizado por el sistema se define como

$W = P Delta V qquad qquad qquad (2)$

Sin embargo, P no permanece constante durante el proceso adiabático sino que por el contrario cambia junto con V.

Deseamos conocer cómo los valores de $Δ P$ y $Δ V$ se relacionan entre sí durante el proceso adiabático. Para ello asumiremos que el sistema es una gas monoatómico, por lo que

$C_{V} = {3 over 2} R$

donde R es la constante universal de los gases.

Dado $Δ P$ y $Δ V$ entonces $W = P Δ V$ y

$Delta U = {3 over 2} n R Delta T = {3 over 2} Delta (P V) = {3 over 2} (P Delta V + V Delta P) qquad (3)$

Ahora sustituyendo las ecuaciones (2) y (3) en la ecuación (1) obtenemos

$-P Delta V = {3 over 2} P Delta V + {3 over 2} V Delta P$

simplificando

$- {5 over 2} P Delta V = {3 over 2} V Delta P$

dividiendo ambos lados de la igualdad entre PV

$-5 {Delta V over V} = 3 {Delta P over P}$

Aplicando las normas del cálculo diferencial obtenemos que

$-5 Delta (operatorname{ln} V) = 3 Delta (operatorname{ln} P)$

que se puede expresar como

${operatorname{ln} P - operatorname{ln} P_0 over operatorname{ln} V - operatorname{ln} V_0 } = -{5 over 3}$

Para ciertas constantes $P 0$ y $V 0$ del estado inicial. Entonces

${operatorname{ln} (P/P_0) over operatorname{ln} (V/V_0)} = -{5 over 3},$

$operatorname{ln} left( {P over P_0} right) = operatorname{ln} left( {V over V_0} right)^{-5/3}$

elevando al exponente ambos lados de la igualdad

$left( {P over P_0} right) = left( {V over V_0} right)^{-5/3}$

eliminando el signo menos

$left( {P over P_0} right) = left( {V_0 over V} right)^{5/3}$

por lo tanto

$left( {P over P_0} right) left( {V over V_0} right)^{5/3} = 1$

$P V^{5/3} = P_0 V_0^{5/3} = operatorname{constante}.$

Representación gráfica de las curvas adiabáticas

Las propiedades de las curvas adiabáticas en un diagrama P-V son las siguientes:

Cada adiabática se aproxima asintóticamente a ambos ejes del diagrama P-V (al igual que las isotermas).
Cada adiabática interseca cada isoterma exactamente una sola vez.
Una curva adiabática se parece a una isoterma, excepto que durante una expansión, una adiabática pierde más presión que una isoterma, por lo que inclinación es mayor (es más vertical).
Si las isotermas son cóncavas hacia la dirección "noreste" (45°), entonces las adiabáticas son cóncavas hacia la dirección "este noreste" (31°).
Si adiabáticas e isotermas se dibujan separadamente con cambios regulares en la entropía y temperatura, entonces a medida que nos alejamos de los ejes (en dirección noreste), parece que la densidad de las isotermas permanece constante, pero la densidad de las adiabáticas disminuye. La excepción se encuentra muy cerca del cero absoluto, donde la densidad de las adiabáticas cae fuertemente y se hacen muy raras

El siguiente esquema representa un diagrama P-V con una superposición de adiabáticas e isotermas.

Las isotermas son las curvas rojas y las adiabáticas son las curvas negras. Las adiabáticas son isentrópicas. El volumen está representado en el eje de abcisas y la presión en el eje de ordenadas.

Procesos adiabáticos en mecánica cuántica

En mecánica cuántica una transformación adiabática es un cambio lento en el Hamiltoniano cuántico $hat H,$ que describe el sistema y que resulta en un cambio de los valores propios del Hamiltoniano pero no de sus estados propios. Por ejemplo, si un sistema comienza en su estado fundamental permanecerá en el estado fundamental a pesar de que las propiedades de este estado pueden cambiar. Si en tal proceso se produce un cambio cualitativo en las propiedades del estado fundamental, como por ejemplo un cambio de spin la transformación se denomina transición de fase cuántica. Las transiciones de este tipo son transiciones de fase prohibidas por la mecánica clásica.